Observemos algumas curvas no plano:

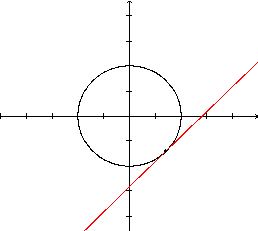
A reta tangente "toca" a curva em um único ponto.

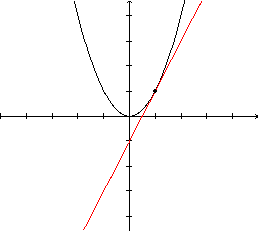
A reta tangente "toca" a curva em um único ponto.

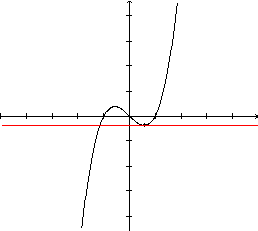
A reta tangente encontra a curva em dois pontos: no ponto em que é tangente, a reta apenas "toca" a curva; no outro ponto, a reta atravessa a curva.

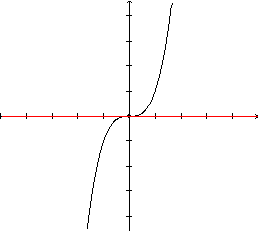
A reta tangente intercepta a curva em um único ponto, sendo que a reta "atravessa" a curva.

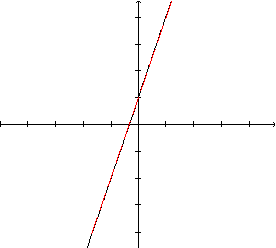A reta tangente a uma reta, em qualquer ponto, é a própria reta!

Nas figuras observamos que o conceito de reta tangente a uma curva é uma questão delicada e a idéia dessa reta encontrar a curva num único ponto não é geral. Isso realmente funciona no caso de uma circunferência e mesmo de uma parábola, mas já não funciona numa curva como aquela da Situação 3, que é o gráfico de uma função polinomial de grau três.
Também não é geral a idéia de que, localmente, a reta apenas toca a curva, sem atravessá-la. De fato, na Situação 4, em y=x³, a reta y=0, que atravessa a curva, é a reta tangente no ponto (0,0).
E, na Situação 5, no caso da curva dada ser uma reta, a reta tangente em qualquer ponto coincide com essa mesma reta!

A característica comum a todas as situações é a de que "perto" do ponto de tangência a reta está "muito próxima" à curva, mas essa idéia se tornará mais precisa.

De modo geral, examinando uma curva e a reta tangente num ponto T dessa curva, observamos que pontos da reta tangente, próximos a T, estão bem perto de pontos da curva, também próximos a T.

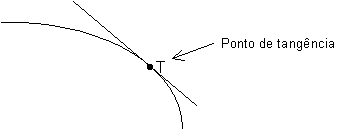
Essas idéias ficarão mais claras quando conseguirmos resolver o seguinte problema: considerando uma curva que é o gráfico de uma função, encontrar a reta tangente a essa curva num ponto estabelecido.