Assim no caso de y=x², temos:

x=x₀ Þ y₀=f(x₀)=x₀²
x=x₀+Dx Þ y=y₀+Dy=f(x₀+Dx)=(x₀+Dx)²

Logo: Dy=(x₀+Dx)² - x₀²=2x₀.Dx+(Dx)²

Observemos que Dy depende do particular valor x₀ e da variação Dx da variável independente, pois Dy=2x₀.Dx+(Dx)².

Em particular, para Dx=0,25 e para diferentes valores de x₀, temos diferentes valores para Dy.

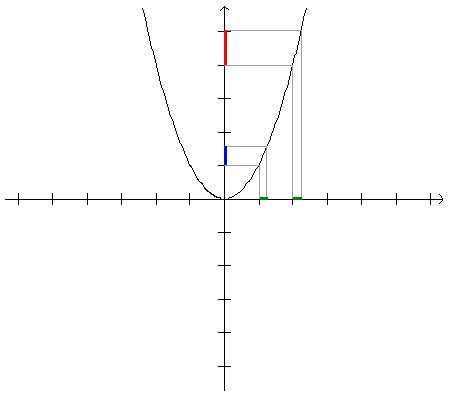
Assim, quando x varia em intervalos diferentes, de igual comprimento, a mesma função y sofre diferentes variações.

Resultados desse tipo não nos dizem muita coisa, pois saber a variação da grandeza y em determinado intervalo, não é de grande utilidade, se não estivermos relacionando essa variação ao tamanho do intervalo.

As variações Dy e Dx das duas grandezas y e x estão inter-relacionadas e, para deixar esse fato explícito, podemos examinar a razão , que, no caso, de y=x², nos fornece:

,

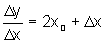uma vez que Dy=2x₀.Dx+(Dx)².