![]()
• A
área de um círculo em função do raio r
é dada por A(r)=pr2,
logo a taxa de variação da área em relação
ao raio é dada por:
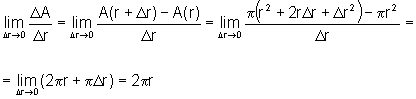
Isso nos diz que a taxa de variação pontual da área do círculo com relação ao seu raio é igual ao comprimento da circunferência.
Uma interpretação
geométrica para esse fato é a de que se o raio sofre um
acréscimo Dr e, em correspondência,
a área do círculo sofre um incremento DA,
então DA é a área da coroa
circular , ao redor do círculo inicial. Quando 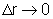 ,
o quociente
,
o quociente 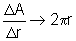 , que
é o comprimento da linha à qual tende a coroa circular considerada.
, que
é o comprimento da linha à qual tende a coroa circular considerada.

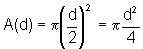 , logo
a taxa de variação da área em relação
ao diâmetro é dada por:
, logo
a taxa de variação da área em relação
ao diâmetro é dada por: 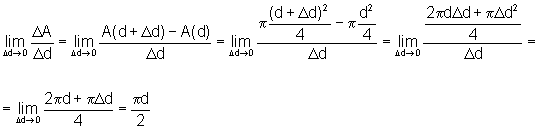
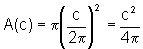 ,
logo a taxa de variação da área em relação
ao comprimento é dada por:
,
logo a taxa de variação da área em relação
ao comprimento é dada por:

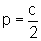 é dada
por
é dada
por 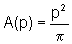 , logo a taxa
de variação da área em relação ao semi-perímetro
é dada por:
, logo a taxa
de variação da área em relação ao semi-perímetro
é dada por: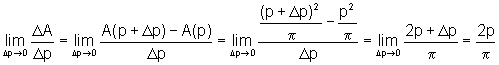
Em cada
caso, a taxa de variação determinada depende do raio, logo
para cada valor dado do raio, teremos uma taxa de variação
da área diferente.
No caso específico de r=1, temos que:
