São dadas: a função 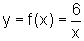e reta 2y+3x+1=0.

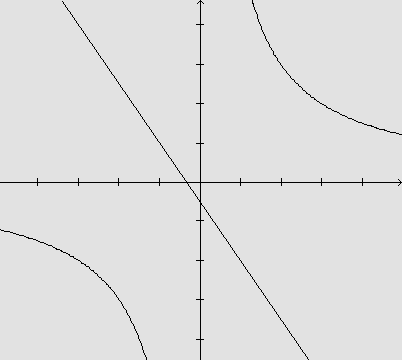
Sabemos que duas retas paralelas possuem o mesmo coeficiente angular. Assim, as retas tangentes procuradas têm o mesmo coeficiente angular que a reta 2y+3x+1=0, que pode ser escrita na forma:

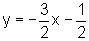
Logo, seu coeficiente angular é .

O coeficiente angular da reta tangente ao gráfico de 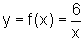num ponto genérico é dado pela derivada da função f na abscissa x, ou seja

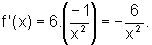
A fim de que a reta tangente procurada seja paralela à reta 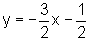, é necessário que:

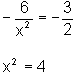
ou seja, x=2 ou x=-2.

Logo os pontos procurados da curva 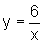são: (2,f(2)) e (-2,f(-2)), ou seja (2,3) e (-2,-3). Graficamente, temos:

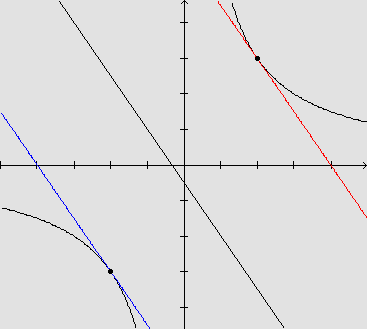
onde as retas encontradas têm equação:

,

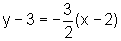ou seja, 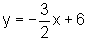que é a reta tangente à curva no ponto (2,3).

e ,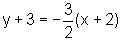

ou seja, 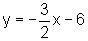que é a reta tangente à curva no ponto
(-2,-3).