Sejam y=h(u) e u=g(x)
duas funções deriváveis, com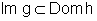 
,
e consideremos a função composta y=f(x)=h[g(x)]. Então
f é derivável e
f '(x)=h'(g(x)).g'(x), para todo x pertencente ao Dom g.
Por hipótese, existem:
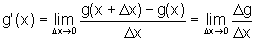e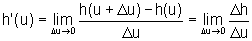 
A tese a ser demonstrada é que existe
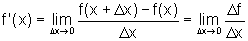
e que f '(x)=h'(g(x)).g'(x), para todo x pertencente ao Dom g.
Demonstração:
Precisamos mostrar que existe o seguinte limite:
.
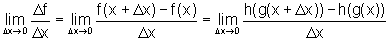
Sendo u=g(x), colocamos
.
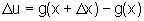Então,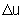 
depende de 
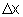e, quando
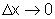, temos 
.
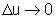Temos assim,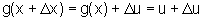 
e podemos escrever:
h(g(x))=h(u) e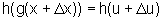 
Assim,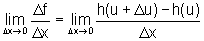 
Suponhamos que
.
Então,
(*)
Quando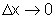 
,
temos 
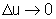, e utilizando
a hipótese, temos:
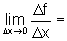h'(g(x)).g'(x), o que completa a prova no caso em que
.
Entretanto, essa
prova não é geral porque para valores arbitrariamente
pequenos 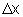de 
poderia
acontecer que o acréscimo fosse zero, o que invalida a última
passagem de (*).
Uma demonstração
para o caso geral que evite a referida passagem pode ser feita, através
de um argumento que, nas palavras do Simmons,
constitui um engenhoso
artifício matemático.
 |
 |