As palavras "equação"
e "diferencial" juntas sugerem que se trata de algum
tipo de equação envolvendo derivadas.
-
Por exemplo, a equação
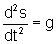é uma equação que descreve o movimento de um
corpo em queda livre sujeito à ação da gravidade.
-
Outro exemplo é a equação diferencial
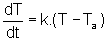que traduz a lei de Newton sobre o resfriamento de um corpo, segundo
a qual a taxa de esfriamento de um corpo é proporcional à
diferença entre a temperatura T do próprio corpo e a
temperatura do meio ambiente Ta.
De modo geral, uma equação diferencial ordinária é uma equação que envolve derivadas de uma variável dependente em relação a uma variável independente.
Nessa conceituação estamos considerando que se y=f(x), a função y - isto é, a variável dependente - é a derivada de ordem zero em relação a x.
Assim, são exemplos de equações diferenciais:
-
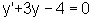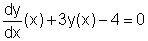
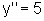que pode ser escrita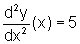 
-
que pode ser escrita 
-
que pode ser escrita 
-
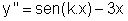que pode ser escrita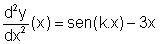 
-
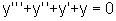que pode ser escrita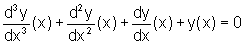 
Resolver uma equação diferencial significa determinar uma função - na verdade, uma família de funções - que satisfazem a equação dada.
A resolução de equações diferenciais ordinárias é um assunto por si só bastante amplo, que não iremos detalhar.
Entretanto, é
interessante saber que a observação de fenômenos
e a busca de explicações para eles, ou a otimização
da solução de um problema constitui o foco central das
situações da modelagem. Um modelo é estabelecido
quando conseguimos descrever o fenômeno ou a situação-problema
através de uma equação diferencial ou de um sistema
de equações diferenciais.
 |
 |