![]()
![]() A função
A função 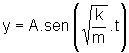 representa as oscilações de uma mola com uma massa m presa
em uma de suas extremidades, sendo k a constante elástica da mola.
representa as oscilações de uma mola com uma massa m presa
em uma de suas extremidades, sendo k a constante elástica da mola.
a) Encontre o instante
no qual a massa está mais distante do seu ponto de equilíbrio.
Encontre o instante no qual a massa está se movimentando com velocidade
máxima. Encontre o instante no qual a massa está se movimentando
com aceleração máxima.
b) Qual é o período T da oscilação?
c) Encontre 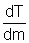 .
O que nos diz o sinal de
.
O que nos diz o sinal de 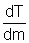 ?
?
![]() Seja a função
Seja a função 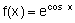 .
Investigue algumas das propriedades de f, através das questões:
.
Investigue algumas das propriedades de f, através das questões:
a) Qual o domínio
de f?
b) f é periódica?
c) f assume valores negativos?
d) f tem raízes?
e) f tem algum valor máximo? E mínimo?
f) f é o resultado da composição de uma função
exponencial com uma função trigonométrica. A função
f cresce infinitamente como uma função exponencial?
g) Qual a imagem de f?
![]() Consideremos a situação onde areia escoa numa ampulheta.
Isto acontece de modo que a areia vá formando um cone na parte
inferior, cujo raio é sempre o triplo da altura. Sabendo que a
taxa de escoamento da areia é constante e é de 50 mm3/s,
determine a taxa de crescimento da altura do cone, após 5 minutos
do início do fenômeno.
Consideremos a situação onde areia escoa numa ampulheta.
Isto acontece de modo que a areia vá formando um cone na parte
inferior, cujo raio é sempre o triplo da altura. Sabendo que a
taxa de escoamento da areia é constante e é de 50 mm3/s,
determine a taxa de crescimento da altura do cone, após 5 minutos
do início do fenômeno.
![]() Seja a função h(x)=f(g(x)), sendo g(x)=cos x. Sabendo que
f'(-1)=3, determine o valor de
Seja a função h(x)=f(g(x)), sendo g(x)=cos x. Sabendo que
f'(-1)=3, determine o valor de 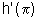 .
.
![]() Dadas as funções
Dadas as funções 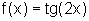 e
e 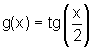 definidas
para
definidas
para 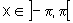 :
:
a) Resolva as equações:
f'(x)=1 e g'(x)=1.
b) Dê uma interpretação gráfica dos resultados
da parte a), em termos das inclinações
dos gráficos das funções f e g.
![]() Resolva a equação
diferencial
Resolva a equação
diferencial 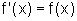 .
.
![]() Obtenha o aumento do volume de uma esfera quando seu raio varia de 3cm
a 3,1cm.
Obtenha o aumento do volume de uma esfera quando seu raio varia de 3cm
a 3,1cm.
![]() Um
terreno, em desapropriação para reforma agrária,
tem a forma de um quadrado. Estima-se que seus lados medem 1500m, com
um erro máximo de 50m. Usando taxa de variação, determine
o possível erro no cálculo da área do terreno.
Um
terreno, em desapropriação para reforma agrária,
tem a forma de um quadrado. Estima-se que seus lados medem 1500m, com
um erro máximo de 50m. Usando taxa de variação, determine
o possível erro no cálculo da área do terreno.
![]() Um tanque de óleo deve ser drenado para limpeza. Sobram V galões
de óleo no tanque t minutos após o início da drenagem,
onde
Um tanque de óleo deve ser drenado para limpeza. Sobram V galões
de óleo no tanque t minutos após o início da drenagem,
onde 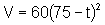 ,
calcule:
,
calcule:
a) a taxa média
em que é drenado o óleo para fora do tanque durante os primeiros
30 minutos.
b) a taxa em que o óleo está fluindo para fora do tanque
30 minutos após o início da drenagem.
![]() Prove que a derivada de uma função
par é uma
função ímpar, bem como a derivada de uma função
ímpar é uma função par.
Prove que a derivada de uma função
par é uma
função ímpar, bem como a derivada de uma função
ímpar é uma função par.
![]() Nos carros de corrida, utiliza-se um pneu de ultra-aderência cuja
consistência é mais macia do que a de um pneu normal e cuja
superfície de contato é plana - pneu slick. Um fabricante
desse tipo de pneus garante que a quantidade de borracha gasta em média,
quando um carro está rodando a 200km/h, é de 1,5cm2/s.
Sabendo que esse pneu, quando novo, tem diâmetro de 45cm e largura
de 30cm, encontre:
Nos carros de corrida, utiliza-se um pneu de ultra-aderência cuja
consistência é mais macia do que a de um pneu normal e cuja
superfície de contato é plana - pneu slick. Um fabricante
desse tipo de pneus garante que a quantidade de borracha gasta em média,
quando um carro está rodando a 200km/h, é de 1,5cm2/s.
Sabendo que esse pneu, quando novo, tem diâmetro de 45cm e largura
de 30cm, encontre:
a) a taxa de variação
do diâmetro do pneu para um carro rodando nessas condições.
b) a taxa de variação do diâmetro quando o pneu, já
usado, estiver com diâmetro de 42,7cm.
![]() Mostre que a função
Mostre que a função 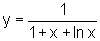 satisfaz a equação
diferencial
satisfaz a equação
diferencial 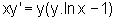 .
.
 |
