Sistema massa-mola: Movimento Harmônico Simples

Suponhamos que um corpo de massa m, apoiado num plano horizontal, sem atrito, esteja preso na extremidade de uma mola, sendo que a outra extremidade da mola está fixada numa parede vertical. O sistema é suposto em condições ideais, sem atrito ou resistência do ar.

Inicialmente temos um sistema em equilíbrio, isto é, a mola não sofre nenhum tipo de deformação.

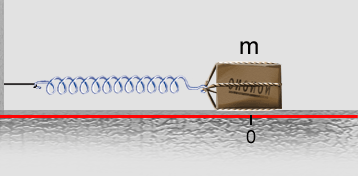
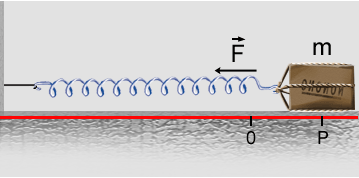
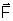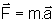Se o corpo é deslocado para uma posição P, esticando a mola, ela passa a exercer sobre corpo uma força de intensidade , dirigida à posição de equilíbrio O do sistema. Assim e o corpo passa a ter uma aceleração 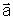em direção à posição de equilíbrio e sua velocidade aumenta em valor absoluto.

A força é proporcional à deformação sofrida pela mola, onde 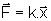, k é a constante elástica da mola e o deslocamento. À medida que o corpo se afasta da posição P em direção ao ponto de equilíbrio O, a intensidade da força vai diminuindo e se anula quando o corpo atinge a posição de equilíbrio. Nesse ponto, portanto, a aceleração é zero.

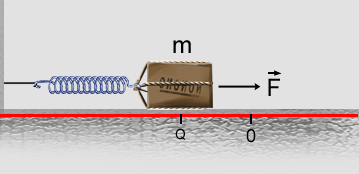
Ao atingir o ponto de equilíbrio a velocidade é máxima e o corpo ultrapassa a posição de equilíbrio, comprimindo a mola. Nesse momento passa a existir uma força sobre o corpo, dirigida para o ponto de equilíbrio e, portanto, em sentido contrário ao da velocidade do corpo. Dessa maneira, o movimento é retardado e na posição Q, simétrica a P, em relação ao ponto de equilíbrio O, a velocidade do corpo se anula.

Partindo de Q o corpo é acelerado para O, ultrapassa esse ponto, sendo então retardado pela mola até alcançar a posição P. Como a situação descrita tem condições ideais, o movimento continua ad infinitum.

Esse movimento é denominado Movimento Harmônico Simples. Ele é descrito pela equação 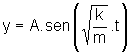, onde:

y: posição do corpo no movimento oscilatório;
A: amplitude da oscilação;
k: constante elástica da mola;
m: massa do corpo;
t: tempo

A distância entre a posição de equilíbrio e a posição extrema ocupada pelo corpo que oscila é denominada amplitude A do movimento.

O tempo que o corpo gasta para efetuar uma oscilação completa - vai de P até Q e retorna a P - é denominado período T do movimento. O número de oscilações completas que o corpo efetua por unidade de tempo é denominado freqüência f do movimento.

Finalmente, se o corpo oscila com uma freqüência f, o seu período de vibração T é dado por 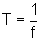.