: Para a função y=f(x)=x³ e o ponto x₀=-1, considere valores negativos para Dx que, sucessivamente se aproximam de zero. Construa uma tabela para concluir que a taxa de variação média se aproxima do valor 3.

Dada a função 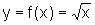e o ponto (4,2) de seu gráfico, use uma calculadora para construir uma tabela relacionando os acréscimos Dx na variável independente x, a partir de x₀=4, tanto positivos como negativos - mas de modo que 4+Dx >0 - e os correspondentes resultados 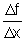. Assim, você estará calculando a taxa de variação média quando x varia no intervalo [4, 4+Dx] se Dx>0, ou [4+Dx ,4] se Dx<0. A variável dependente y assume qualquer valor, respectivamente, no intervalo [2, f(4+Dx)] ou [f(4+Dx ), 2], pois f(4)=2.

Encontre o valor do 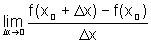, quando x₀=4.

A seguir, escreva a equação da reta tangente ao gráfico de no ponto (4,2). Verifique algebricamente que a reta encontrada intercepta o gráfico da função apenas no ponto (4,2).

Determine a equação da reta que é tangente à parábola de equação y=2x²+3 e que é paralela à reta de equação y=8x+3.

Determine as retas que passam por (1,4) e que tangenciam a parábola y=4-x².

Para que valores de a e b a parábola y=ax²+b tangencia a reta y=x?