![]()
Vamos examinar, cuidadosamente,
a questão da translação horizontal, através
de um gráfico.
Seja A=(x0,h(x0))
um ponto do gráfico y=h(x).

Observemos que, para m >0, temos:
- O gráfico
de y=h(x+m) sofreu uma translação
horizontal de -m em relação
ao gráfico de y=h(x). Assim, o ponto B
do gráfico de y=h(x+m) tem coordenadas B=(x0-m,
h(x0)), ou também
podemos pensar em B=(x1,
h(x1+m)),
com x1=x0-m.
- O gráfico de y=h(x-m) sofreu uma translação horizontal de m em relação ao gráfico de y=h(x). Assim, o ponto C do gráfico de y=h(x-m) tem coordenadas C=(x0+m, h(x0)), ou também podemos pensar em C=(x2, h(x2-m)), com x2=x0+m.
Examinando as retas tangentes, temos:
- A reta tangente
ao gráfico de y=h(x+m) no ponto B=(x1,
h(x1+m)) é paralela à
reta tangente ao gráfico de y=h(x) no ponto A=(x0,
h(x0)).
- A reta tangente ao gráfico de y=h(x+m) no ponto C=(x2, h(x2+m)) é paralela à reta tangente ao gráfico de y=h(x) no ponto A=(x0, h(x0)).
Assim, temos:
- O coeficiente angular
da reta tangente ao gráfico de y=h(x+m) no ponto de abscissa
x1=x0-m
é h'(x0); ou, de outra
maneira, no ponto de abscissa x1 é
h'(x1+m). É interessante observar
que quando um gráfico sofre uma translação horizontal
de -m unidades, onde m>0,
a reta tangente a esse gráfico, evidentemente, sofre a mesma
translação horizontal e o ponto de tangência que
era do tipo (a, h(a)), passa a ser (a-m,h(a)).
- O coeficiente angular da reta tangente ao gráfico de y=h(x-m) no ponto de abscissa x2=x0+m é h'(x0); ou, de outra maneira, no ponto de abscissa x2 é h'(x2-m). Observamos que, quando o gráfico sofre uma translação horizontal de m unidades, onde m>0, a reta tangente a esse gráfico, evidentemente, sofre a mesma translação horizontal e o ponto de tangência que era do tipo (a, h(a)), passa a ser (a+m,h(a)).
Conclusão: Sendo m>0:
- Dada uma função y=h(x), considerando uma outra função f(x)=h(x+m), resultado de uma translação horizontal de -m, então f'(x)=h'(x+m).
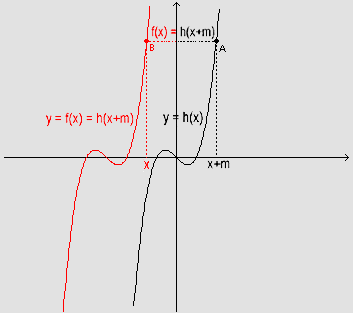
Isso significa que o coeficiente angular da reta tangente ao gráfico
da função transladada no ponto (x,f(x))=(x,h(x+m)) é
igual ao coeficiente angular da reta tangente ao gráfico da função
h original em (x+m, h(x+m)).
De maneira análoga, dada uma função y=h(x), considerando uma outra função g(x)=h(x-m), resultado de uma translação horizontal de m, então g'(x)=h'(x-m).
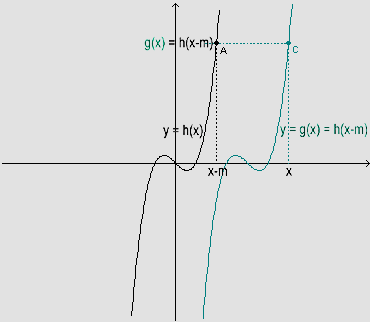
Isso significa que o coeficiente angular da reta tangente ao gráfico da função transladada no ponto (x, g(x))=(x, h(x-m)) é igual ao coeficiente angular da reta tangente ao gráfico da função h original, em (x-m, h(x-m)).
