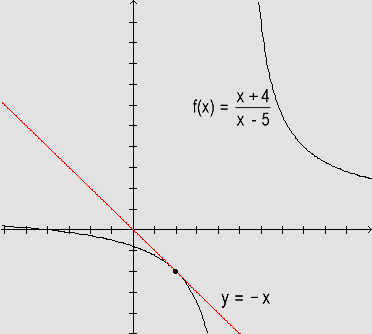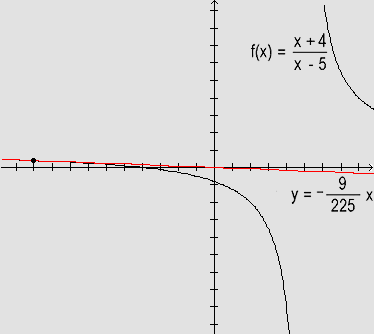Sendo ,

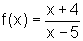temos .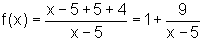

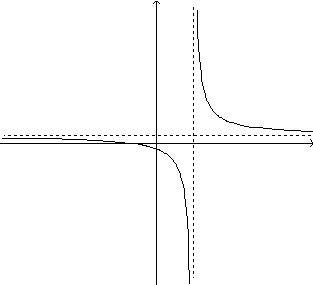
Ainda de modo análogo ao do Exercício 4, temos que, calculando a derivada da função num ponto de abscissa x, qualquer, mas diferente de 5, .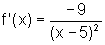

Como vimos, em cada abscissa x₀, 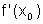é o coeficiente angular da reta tangente ao gráfico no ponto de tangência .

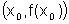Queremos as equações de todas as retas tangentes à curva e que passam pela origem, (0, 0), as quais devem ter a seguinte equação:

y-0=m(x-0),

onde .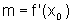

Temos então que 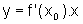é a equação de cada uma das retas procuradas. Como cada uma delas passa pelo ponto 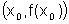, temos:

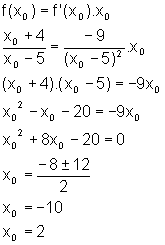
Dessa forma, encontramos dois valores para 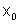, ou seja, temos dois pontos (-10,f(-10)) e (2,f(2)) do gráfico de f que são pontos de tangência. Em cada um deles, existe uma reta passando pela origem, que é tangente à curva.

Quando 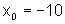, temos ,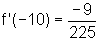

e quando 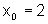, temos .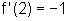

As equações procuradas são, portanto:

y=-1(x-0) ® y=-x

e
y-0= (x-0)® y= 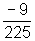x.

Graficamente, temos: