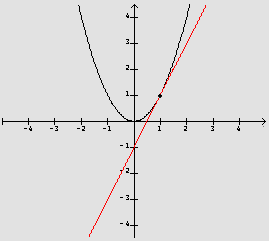
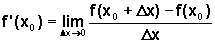![]() Consideremos y=f(x)=x2. O coeficiente
angular da reta tangente ao gráfico de f no ponto (1,1) é
2.
Consideremos y=f(x)=x2. O coeficiente
angular da reta tangente ao gráfico de f no ponto (1,1) é
2.
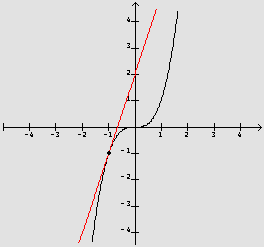
![]() Consideremos agora y=f(x)=x3. O coeficiente
angular da reta tangente ao gráfico de f no ponto (-1,-1)
é 3.
Consideremos agora y=f(x)=x3. O coeficiente
angular da reta tangente ao gráfico de f no ponto (-1,-1)
é 3.
Vamos considerar a situação geral, para chegar a uma conclusão
também geral.
A taxa
de variação média de uma função num
intervalo [x0,x0+Dx]
contido em seu domínio, é o quociente 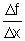 .
Geometricamente, o significado desse quociente, como podemos ver na figura,
é o coeficiente angular da reta que passa pelos pontos (x0,f(x0))
e (x0+Dx,
f(x0+Dx)).
Uma vez que esses dois pontos pertencem ao gráfico da função,
dizemos que essa reta é secante ao gráfico. Observemos que
o coeficiente angular da reta é a
tangente trigonométrica do ângulo - medido no sentido
anti-horário - que a reta forma com o eixo horizontal.
.
Geometricamente, o significado desse quociente, como podemos ver na figura,
é o coeficiente angular da reta que passa pelos pontos (x0,f(x0))
e (x0+Dx,
f(x0+Dx)).
Uma vez que esses dois pontos pertencem ao gráfico da função,
dizemos que essa reta é secante ao gráfico. Observemos que
o coeficiente angular da reta é a
tangente trigonométrica do ângulo - medido no sentido
anti-horário - que a reta forma com o eixo horizontal.
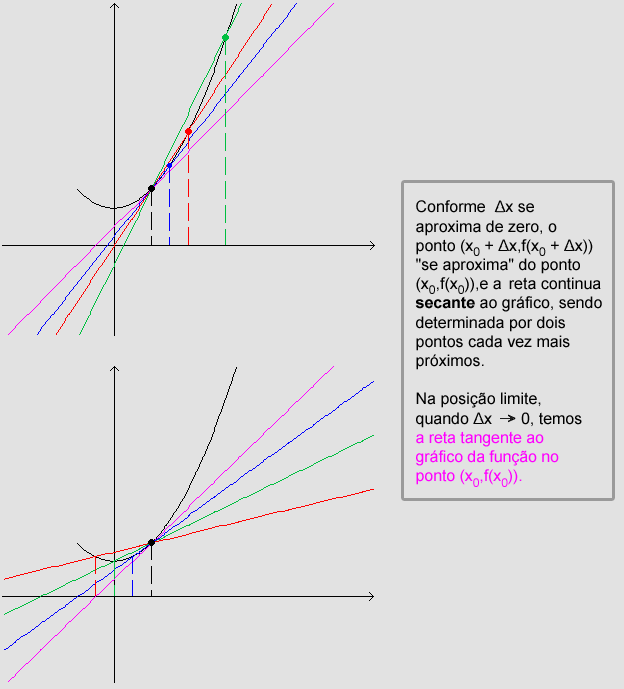
Quando fazemos Dx®0,
a reta secante genérica tende à posição limite
de reta tangente ao gráfico de f no ponto (x0,
f(x0)) e o quociente 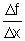 tende ao coeficiente angular da reta em sua posição limite.
tende ao coeficiente angular da reta em sua posição limite.
Dessa maneira, dizemos que, se existe e é finito o limite,
ele é o coeficiente
angular da reta tangente ao gráfico de y=f(x) no ponto de abscissa
x0, isto é, (x0,
f(x0)) é o ponto de tangência.
Chamando q o ângulo que a reta tangente
forma com o eixo horizontal, medido no sentido anti-horário, temos:
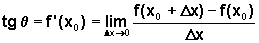
Finalmente, como a equação da reta que passa por um ponto (x0,y0) e tem coeficiente angular m é dada por
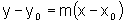
podemos, através da taxa de variação instantânea da função num ponto de seu domínio, obter a equação da reta tangente ao gráfico da função no ponto (x0, f(x0)), que é, portanto: