![]()
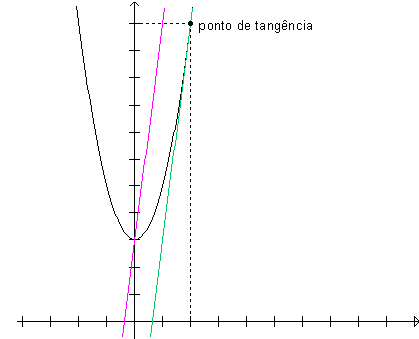
Dada a parábola de equação y=2x2+3, procuramos a equação da reta que é tangente à curva e é paralela à reta y=8x+3. Graficamente, temos:
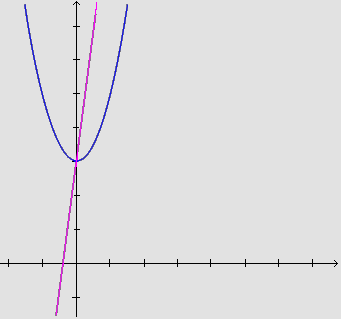
- Em primeiro lugar deve estar claro que não temos o ponto de
tangência e precisamos determiná-lo, a fim de poder escrever
a equação da reta procurada.
- Em segundo lugar, sabemos que o coeficiente angular da reta procurada é 8, devido à condição de paralelismo das duas retas.
- Finalmente, pela definição do coeficiente angular da reta tangente num ponto genérico (x0, f(x0)), temos:
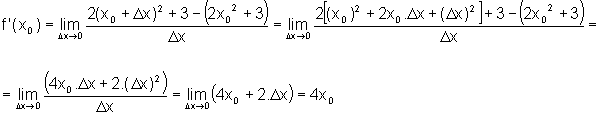
Logo,
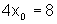
e, portanto, x0=2 é a abscissa do ponto de tangência, sendo que (2, f(2))=(2,11) é o ponto de tangência.
A equação da reta procurada é então a seguinte:

Num gráfico, temos: