Teorema
da Função Inversa: Seja f inversível com inversa
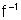 . Se f
for derivável em
. Se f
for derivável em 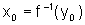 com
com 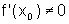 , e
se
, e
se 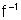 for
contínua em y0, então será
derivável em y0, com
for
contínua em y0, então será
derivável em y0, com 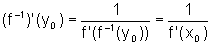 .
.
Demonstração:
Como queremos provar
que existe a derivada de 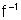 no ponto y0, vamos examinar o quociente:
no ponto y0, vamos examinar o quociente:
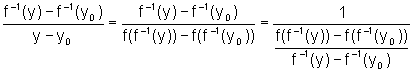 sempre que
sempre que 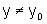 .
.
Seja 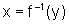 ,
como
,
como 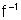 é
contínua
em y0, temos que
é
contínua
em y0, temos que 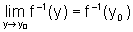 ,
ou seja, quando
,
ou seja, quando 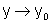 ,
,
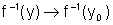 , isto
é,
, isto
é, 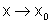 .
Então:
.
Então:
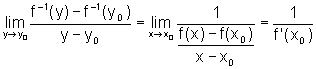
pois f é derivável
em 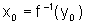 com
com
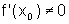 .
.
Logo, mostramos que
existe 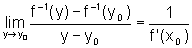 ,
ou seja
,
ou seja 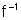 é derivável em
é derivável em 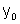 e
e
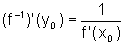
como queríamos demonstrar.
