Sendo x2+y2=1, observamos que o gráfico é
uma circunferência de centro na origem e raio 1, não sendo
portanto o gráfico de uma função.
Entretanto, a equação
dada define y como função implícita de x, que, no
caso, pode ser tornada explícita, fornecendo 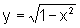 ,
se
,
se 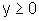 ou
ou 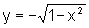 ,
se
,
se 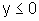 .
.
Para deixar claro
que y é uma função dada implicitamente pela equação,
escrevemos 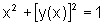 .
.
Derivando ambos os membros da equação com relação à variável x, obtemos:
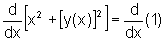
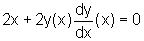
pois não podemos esquecer da Regra da Cadeia.
Isolando a derivada
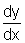 , chegamos a
, chegamos a
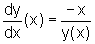 isto é,
isto é, 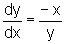
de onde percebemos
que essa derivada existe nos pontos em que y não é zero,
ou seja, 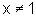 e
e 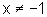 .
.
Se desejarmos exprimir
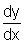 em função
de x unicamente, devemos substituir o valor de y na equação.
em função
de x unicamente, devemos substituir o valor de y na equação.
Assim, 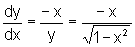 para y>0.
para y>0.
e
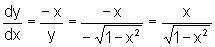 para y<0.
para y<0.
No presente caso,
em que havia sido possível explicitar a variável y, poderíamos
ter calculado a derivada diretamente, e teríamos chegado ao
mesmo resultado.
