O Teorema do Valor Médio

Teorema: Se f é uma função contínua em [a,b] e derivável em ]a,b[ então existe c pertencente a ]a,b[ tal que a reta tangente ao gráfico de f traçada pelo ponto (c,f(c)) é paralela à reta que passa por (a,f(a)) e (b,f(b)), isto é, .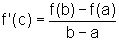

Demonstração:

Consideremos primeiramente, a reta que passa pelos pontos (a, f(a)) e (b, f(b)), isto é:

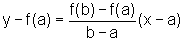
Essa reta é o gráfico da função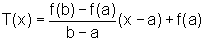

Seja g a função que é a diferença entre f e T, isto é g(x)=f(x) -T(x). Assim,

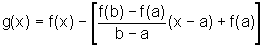
Quando x=a, temos:

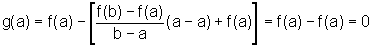
e, quando x=b, temos:

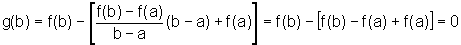
Além disso, como g é a diferença entre duas funções contínuas em [a, b] e deriváveis em ]a, b[, ela própria é contínua em [a, b] e derivável em ]a, b[. Logo podemos usar o Teorema de Rolle para g, concluindo que existe um número c no intervalo ]a, b[, tal que:

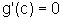
Ou, como ,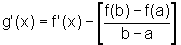

temos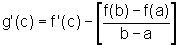

e, portanto,

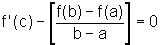
isto é

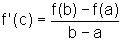
como queríamos provar.

Temos uma primeira conseqüência do TVM, que relaciona o sinal da primeira derivada da função com o seu crescimento/decrescimento.

Seja f uma função contínua num intervalo I, que pode ser aberto ou fechado.
a) Se f '(x)>0 para todo x interior a I, então f será estritamente crescente em I.
b) Se f '(x)<0 para todo x interior a I, então f será estritamente decrescente em I.

Demonstração:

a) Precisamos provar que quaisquer que sejam x₁ e x₂ em I, com x₁<x₂, temos f(x₁)<f(x₂).

Sejam então x₁ e x₂ em I, com x₁<x₂: por hipótese, f é contínua em [x₁,x₂], e derivável em todo ponto interior a esse intervalo. Logo, pelo TVM, existe 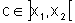tal que .
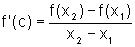Logo, como f '(c)>0, temos: 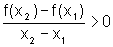e, como x₁<x₂, temos 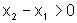e,

portanto, .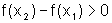

Assim, 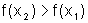como queríamos provar.

b) A demonstração nesse caso é completamente análoga.

Uma segunda conseqüência do TVM relaciona o sinal da segunda derivada da função com a concavidade de seu gráfico.

Seja f uma função derivável pelo menos até segunda ordem num intervalo aberto I.
a) Se f''(x)>0 em I, então o gráfico de f terá concavidade para cima em I.
b) Se f''(x)<0 em I, então o gráfico de f terá concavidade para baixo em I.

Demonstração:

a) Seja a um ponto qualquer do intervalo I. Precisamos mostrar que, para to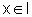do , sendo 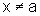, temos f(x)>T(x), onde T é a função cujo gráfico é a reta tangente ao gráfico de f no ponto (a,f(a)), isto é:

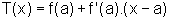
Consideremos a função g, tal que 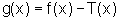, definida para todo .
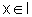Precisamos mostrar então que g(x)>0 para todo , .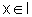

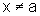Temos:

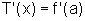
e, como,

,

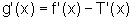então

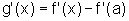, para .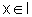

Como, por hipótese, f''(x)>0 em I, segue que, pela primeira conseqüência do TVM, a função f ' é estritamente crescente em I.

Logo,

para x>a, 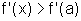e, portanto ;

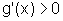para x<a, 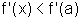e, portanto .

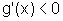Novamente, pela primeira conseqüência do TVM, aplicada à função g, temos que:

para x>a, g é estritamente crescente;

e para x<a, g é estritamente decrescente.

Como g(a)=0, temos g(x)>0 para todo x diferente de a.