![]()
Dois corredores, de larguras a e b, encontram-se num ângulo reto, como indica a figura. Seja l o comprimento máximo de uma viga que pode passar horizontalmente de um corredor para o outro. Determinemos l em termos de a e b.
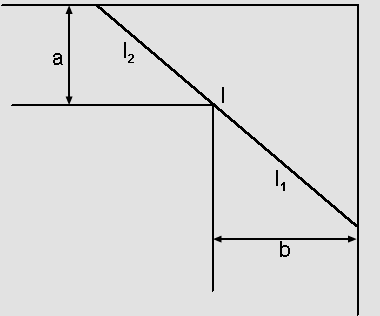
Este problema exige uma observação inicial. Se a viga for muito curta, claramente ela passa; se for muito comprida não passa. Quem já mudou de casa, sabe que esse problema existe, por exemplo, quando é preciso passar uma mesa que não pode ser desmontada por um canto da casa!
A questão é a de determinar, dentre as vigas que não passam, qual é a de comprimento mínimo que passa pelo referido canto.
O comprimento da viga
pode ser escrito como 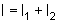 ,
onde
,
onde
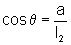 e
e 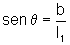 .
.
Portanto o comprimento l é uma função do ângulo q:
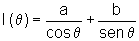 ,
sendo
,
sendo 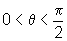
Observação: nas extremidades do intervalo acima, a função não está definida.
Vamos estudar agora a função
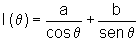 ,
,
para encontrar seu ponto de mínimo.
Temos:
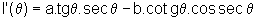
ou,
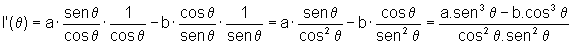
ou ainda
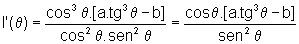
de onde, como
no intervalo considerado, 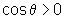 ,
,
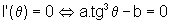
ou seja
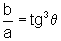
de onde, 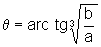
isto é 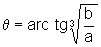 é ponto crítico para a função l.
é ponto crítico para a função l.
Esse ponto é o ponto de mínimo local para a função l, pois:
se 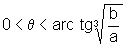 então
então 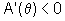 e, portanto, A é estritamente
decrescente;
e, portanto, A é estritamente
decrescente;
se 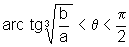 então
então 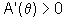 e, portanto, A é estritamente
crescente.
e, portanto, A é estritamente
crescente.
Esse ponto é
um ponto de mínimo global para a função l
no intervalo 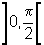 ,
pois a função l não muda seu comportamento
com relação ao crescimento/decrescimento nesse intervalo.
,
pois a função l não muda seu comportamento
com relação ao crescimento/decrescimento nesse intervalo.
Logo o comprimento da viga procurada é:
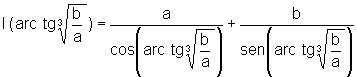 .
.
Assim, ao fazer sua
próxima mudança, você pode saber antes quais os objetos
que deverão passar pela janela!
