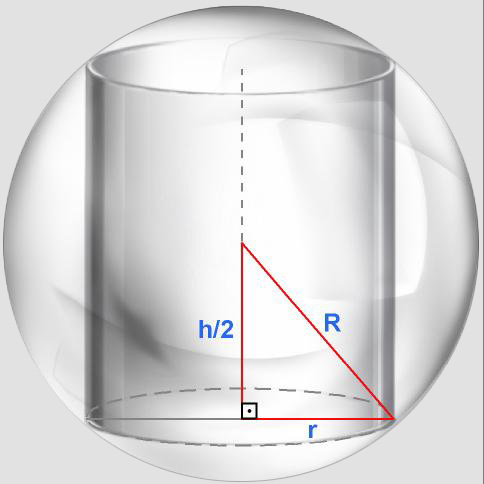
Dada uma esfera de raio R, determine as dimensões do cilindro reto de maior área lateral que pode ser nela inscrito.

A área lateral de um cilindro é dada por:

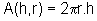
que é uma função de h e r.

Como 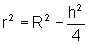, temos:

,

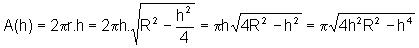que descreve a área da superfície lateral do cilindro de altura h, inscrito na esfera de raio R dado.

Vamos estudar agora a função A, de uma variável h, para 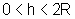, e procurar seu ponto de máximo.

Temos:

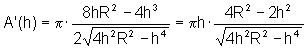
de onde,

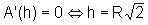
ou seja

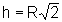é ponto crítico para a função A.

Esse ponto é o ponto de máximo local para a função A, pois:

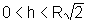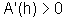se então e, portanto, A é estritamente crescente;

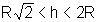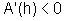se então e, portanto, A é estritamente decrescente.

Esse ponto é um ponto de máximo global para a função A no intervalo , pois a função A não muda seu comportamento com relação ao crescimento/decrescimento nesse intervalo.

Quando 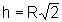o raio do cilindro inscrito na esfera pode ser determinado, uma vez que .

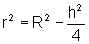Daí encontramos que 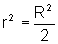, ou seja, 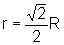.