Demonstre que o retângulo de área máxima, inscrito num círculo de raio r, é um quadrado.

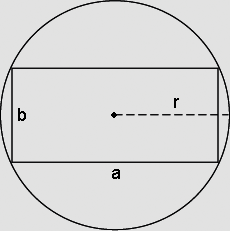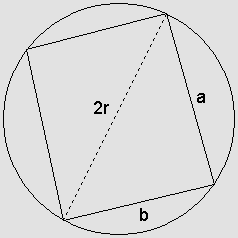
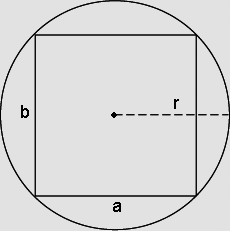
Sendo r o raio da circunferência, sejam a e b os lados do retângulo inscrito, de modo que sua área é dada por:

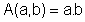
ou seja, a função A depende das variáveis a e b.

Pelo Teorema de Pitágoras, temos que:

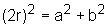, ou seja, .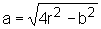

Substituindo na expressão que fornece a área, temos:

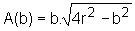
e, dessa maneira, A é função de uma única variável: b, sendo .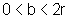

Observação: Se b=0 ou b=2r, temos retângulos "degenerados".

Vamos estudar agora a função

,

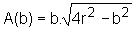para encontrar seu ponto de máximo.

Temos:

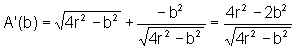
ou seja,

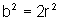
isto é 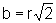é ponto crítico para a função A.

Esse ponto é um ponto de máximo local para a função A, pois:

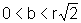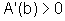se então e, portanto, A é estritamente crescente;

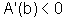se então e, portanto, A é estritamente decrescente.

Esse ponto é o ponto de máximo global para a função A no intervalo ]0,2r[, pois a função A não muda seu comportamento com relação ao crescimento/decrescimento nesse intervalo.

Substituindo em 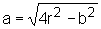, temos:

.

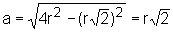Portant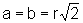o, ou seja, o retângulo de área máxima inscrito numa circunferência é um quadrado.