Problemas de otimização

Para resolver este tipo de problema, são necessários pelo menos alguns cuidados:

• Estabelecer uma função que esteja envolvida no problema, identificando as variáveis independentes e a variável dependente.
•Transformar essa função numa função de uma única variável, a partir dos dados do problema.
• Determinar o(s) ponto(s) crítico(s) para a função, no intervalo em que a mesma tem sentido no contexto do problema.
• O ponto crítico não é automaticamente a solução do problema: é preciso fazer uma análise para garantir qual é a solução. Além de tudo, podem existir problemas sem solução.

Demonstre que o retângulo de área máxima inscrito num círculo de raio r é um quadrado.

Determine o retângulo de área máxima inscrito em um semicírculo, de forma que um de seus lados esteja sobre o diâmetro.

Dois corredores, de larguras a e b, encontram-se em ângulo reto. Seja l o comprimento máximo de uma viga que pode passar horizontalmente de um corredor para o outro. Determine l em termos de a e b.

Encontre sobre a curva 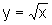o ponto que está mais próximo de (a,0), onde a>0.

Considere n medidas x₁, x₂, ..., x_n de uma certa grandeza x e os erros x₁-x, x₂-x, ..., x_n-x. Mostre que o valor de x que minimiza a soma dos quadrados dos erros é a média aritmética.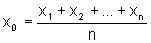

Deseja-se construir um canal, cuja seção transversal seja um trapézio, onde a base e as paredes laterais têm largura fixada a. Calcule o ângulo q de inclinação das paredes laterais para que o canal dê a máxima vazão.

Encontre, quando existirem, os extremos das funções abaixo, bem como os pontos onde eles ocorrem

a)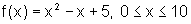

b)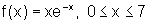

c)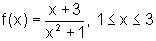

d)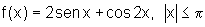

e)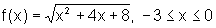

Decida se as afirmações abaixo são verdadeiras ou falsas. Se verdadeiras, demonstre. Se falsas, dê um contra-exemplo.

a) Se uma função f definida em [a,b] assume seu valor mínimo em a e seu valor máximo em b, então f é crescente.

b) Se 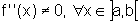então f assume seus valores máximo e mínimo nos extremos de [a,b].

Dada uma esfera de raio R, determine as dimensões do cone reto de volume máximo que pode ser nela inscrito.

Dada uma esfera de raio R, determine as dimensões do cone reto de área lateral máxima que pode ser nela inscrito.

Dada uma esfera de raio R, determine as dimensões do cilindro reto de volume máximo que pode ser nela inscrito.

Dada uma esfera de raio R, determine as dimensões do cilindro reto de maior área lateral que pode ser nela inscrito.

Quais as dimensões do cone de volume mínimo que pode ser circunscrito a uma esfera de raio R?