O crescimento/decrescimento de uma função num intervalo contido em seu domínio e os pontos de extremo
A noção intuitiva de crescimento/decrescimento de uma função num intervalo aberto, contido em seu domínio, nos faz pensar num determinado tipo de gráfico. Entretanto, é preciso tomar muito cuidado com as definições abaixo.
Definição:
Uma função f é dita crescente num intervalo I quando
para qualquer par de pontos x1 e x2,
com x1< x2,
tem-se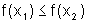 
.
Definição:
Uma função f é dita decrescente num intervalo I quando
para qualquer par de pontos x1 e x2,
com x1< x2,
tem-se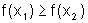 
.
Definição:
Uma função f é dita estritamente crescente num intervalo
I quando para qualquer par de pontos x1
e x2, com x1<
x2, tem-se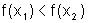 
.
Definição:
Uma função f é dita estritamente decrescente num
intervalo I quando para qualquer par de pontos x1
e x2, com x1<
x2, tem-se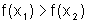 
.
Todas são definições simples. O cuidado a ser tomado é com o quantificador: "qualquer que seja". Assim, para provar que determinada função é crescente num intervalo não basta provar que:
se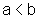 
então 
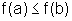
é preciso se certificar de que ficou estabelecido que a e b são quaisquer no intervalo considerado.
Através da noção de crescimento/decrescimento de uma função num intervalo aberto, podemos definir o ponto de extremo da função nesse intervalo.
Definição:
Seja I um intervalo aberto, tal que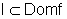 
e seja 
.
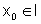Dizemos que x0 é um ponto de
máximo local para f quando existe uma vizinhança V ao
redor de x0 tal que 
,
para todo x pertencente a V. Analogamente, x0
é um ponto de mínimo local para f quando existe uma
vizinhança V ao redor de x0 tal
que 
,
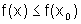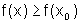para todo x pertencente a V.
Nem sempre existe algum ponto de máximo ou de mínimo e, quando existe, não necessariamente é único.
O ponto x0
é um ponto de máximo glob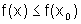al quando
para todo x pertencente a Dom f. Analogamente, o ponto x0
é um ponto de mínimo global quando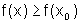
para todo x pertencente a Dom f.
Observação: De acordo com as definições acima, uma função constante é tanto crescente como decrescente. Também, qualquer um dos pontos de seu domínio pode ser considerado um ponto de máximo ou de mínimo.
Vamos analisar a maneira pela qual esses conceitos se relacionam com a função derivada.
Dado o gráfico de uma função f qualquer, podemos
esboçar o gráfico da função derivada f'
?
Analogamente podemos esboçar, a partir do gráfico da função
derivada f', o gráfico de f?
Se uma função é estritamente crescente em um intervalo
dado, então a sua derivada é estritamente positiva?
Se uma função é estritamente decrescente em um intervalo
dado, então a sua derivada é estritamente negativa?
Se f'(x0)=0, ou seja, a reta tangente
ao gráfico de f no ponto (x0,f(x0))
é horizontal, então x0
é um ponto de extremo para f?
Vimos que as afirmações da Situação 3 e da Situação 4 são falsas, entretanto, as recíprocas dessas afirmações são verdadeiras, ou seja:
Toda
função com derivada estritamente positiva em um intervalo
I é estritamente crescente em I.
Toda função com derivada estritamente negativa em um intervalo
I é estritamente decrescente em I.
Essas duas últimas afirmações são muito úteis para a construção do gráfico de uma função e elas são conseqüências do Teorema do Valor Médio.
A recíproca da Situação 5 também é verdadeira e pode ser colocada precisamente da seguinte maneira:
Propriedade: Seja f uma função contínua com um máximo ou um mínimo local num ponto x0, no qual f é derivável. Então f'(x0)=0, isto é, x0 é um ponto crítico para f, ou seja, a reta tangente ao gráfico de f no ponto (x0,f(x0)) é horizontal.
 |
 |