Sendo 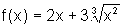, temos:

i) O domínio: Dom f=R

ii) Intersecções com os eixos:

Quando x=0, temos y=0.

Por outro lado, y=0 se e somente se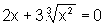

ou seja,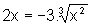

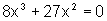, e, portanto, x=0 ou .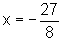

iii) A primeira derivada:

Como 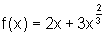, temos:

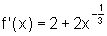ou seja , .

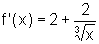Logo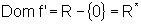

iv) Pontos críticos, isto é, pontos que anulam a primeira derivada:

Temos f'(x)=0 se e somente se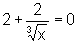
ou seja,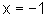

que é o único ponto crítico.

v) Estudo do sinal da primeira derivada:

Temos:

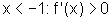logo, f é estritamente crescente;

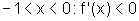logo, f é estritamente decrescente;

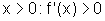logo, f é estritamente crescente;

Logo, é um ponto de máximo local;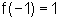

vi) A segunda derivada:

Como 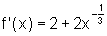, temos:

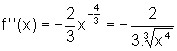
Logo .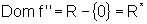

vii) Pontos que anulam a segunda derivada:

Observamos que 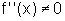para todo x pertencente ao domínio de f''.

viii) Estudo do sinal da segunda derivada:

Observamos que 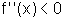para todo x pertencente ao domínio de f'', logo o gráfico de f apresenta concavidade sempre voltada para baixo. Portanto, não há ponto de inflexão.

ix) Limites nas extremidades dos intervalos que constituem o domínio da função:

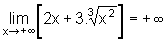
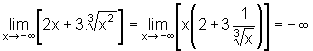
x) O gráfico da função:

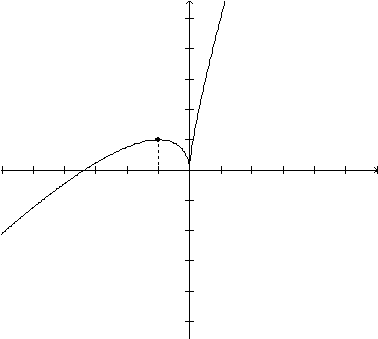
No gráfico, podemos observar o ponto 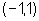que é ponto de máximo local. Observamos também que não há mudança de concavidade. Também observamos que a função não é derivável em x=0.