Segundo Boyer, Fermat fez uma importante descoberta que foi descrita em um tratado que não foi publicado durante sua vida, chamado Método para achar Máximos e Mínimos. Fermat estivera considerando lugares dados - em notação moderna - por equações da forma y=xⁿ; por isso freqüentemente chamadas "parábolas de Fermat" se n>0 ou "hipérboles de Fermat" se n<0. Para curvas polinomiais da forma y=f(x) ele notou um modo muito engenhoso para achar pontos em que a função assume um máximo ou um mínimo. Ele comparou o valor de f(x) num ponto com o valor de f(x+E) num ponto vizinho. Em geral, esses valores serão bem diferentes, mas num alto ou num baixo de uma curva lisa a variação será quase imperceptível. Portanto, para achar os pontos de máximo e de mínimo, Fermat igualava f(x) e f(x+E), percebendo que os valores, embora não exatamente iguais, são quase iguais. Quanto menor o intervalo E entre os dois pontos, mais perto chega a pseudo-equação da verdadeira equação; por isso Fermat, depois de dividir a diferença f(x+E)-f(x) por E, fazia E=0. Os resultados lhe davam as abscissas de máximo e mínimo do polinômio.

Evidentemente, Fermat não tinha o conceito de limite, embora o que ele estivesse fazendo equivalesse a achar .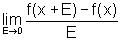

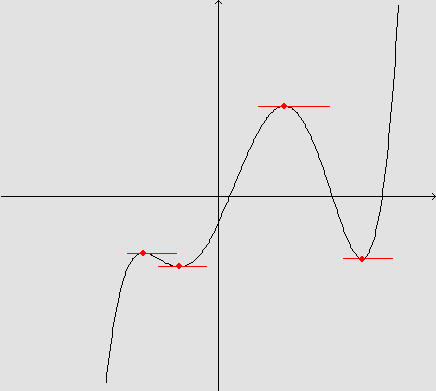
A idéia de Fermat era a de que nos pontos em que a reta tangente é horizontal e o gráfico da função apresenta um "poço" ou um "morro", temos um ponto de mínimo ou de máximo para a função.

Ou seja, nos valores da variável independente x para os quais:

• a derivada da função é nula - isto é, o coeficiente angular da reta tangente é zero;
• a função muda seu comportamento - antes é decrescente e depois é crescente, ou antes é crescente e depois é decrescente, temos, respectivamente, um ponto de mínimo ou de máximo para a função.

Essas idéias podem tornar-se mais precisas com o Teorema do Valor Médio, que é um dos teoremas centrais do curso Cálculo Diferencial e Integral. Entretanto, mesmo sem uma precisão total, podemos perceber que a existência de reta tangente ao gráfico de uma função e o sinal do coeficiente angular dessa tangente nos fornece informações importantes sobre o comportamento da função.