A Situação 11 pode ser generalizada para duas funções que são uma a inversa da outra, desde que, por hipótese, uma delas seja derivável, com derivada diferente de zero.
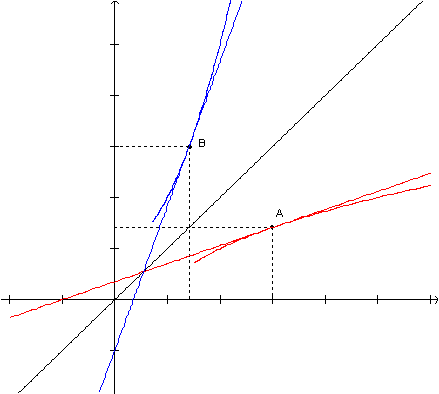
Sejam A=(x1, f(x1)) e B=(x2, g(x2))=(f(x1), x1) os pontos de tangência aos gráficos de y=f(x) e y=g(x)=f-1(x), respectivamente.
A reta tangente ao gráfico de f no ponto A=(x1, f(x1)) tem coeficiente angular f'(x1) e a reta tangente ao gráfico de g no ponto B=(x2, g(x2)) tem coeficiente angular g'(x2).
A questão é descobrir qual a relação entre f'(x1) e g'(x2), sendo (x2, g(x2))=(f(x1), x1) e g(x)=f-1(x), para todo x em que existe a função inversa de f.
Seja q o ângulo determinado pela reta
tangente ao gráfico de f no ponto
A=(x1,
f(x1)); logo 
.
Por simetria,
em relação à reta y=x, o ângulo determinado
pela reta tangente ao gráfico de g no ponto B=(x2,g(x2))
é 
e, portanto,
.
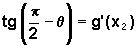Examinando a situação
na circunferência
trigonométrica, temos:
Considerando q =AÔT no triângulo
AOT, temos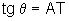 
.
No triângulo AOT', temos que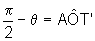 
e, portanto, 
,
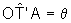pois, nesse triângulo, o ângulo de vértice no ponto
A é reto e, conseqüentement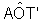e, 
e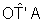 
são
complementares. Logo, nesse triângulo,
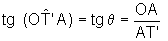e 
e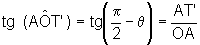, portanto,
Assim, como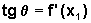 
e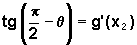 
, temos:
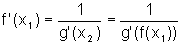
ou ainda,
Assim, se f é inversível e é derivável em x1, com derivada diferente de zero, então sua inversa é derivável em f(x1) e tem por derivada nesse ponto, o inverso da derivada de f em x1.
 |
 |