
se ![]() e que, se
e que, se ![]() .
.
É possível provar que se f(x)=x2+k,
onde k é uma constante, então f'(x)=2x. Qual o significado
desse fato?
![]() Se
Se 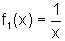 então
então
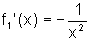 . É
possível generalizar esse fato, ou seja, se
. É
possível generalizar esse fato, ou seja, se 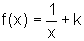 ,
onde k é uma constante, então
,
onde k é uma constante, então 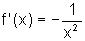 ?
?
![]() De modo geral, se f(x)=h(x)+k, onde k é uma constante, então
a derivada de f coincide com a derivada de h, em todo ponto em que h for
derivável.
De modo geral, se f(x)=h(x)+k, onde k é uma constante, então
a derivada de f coincide com a derivada de h, em todo ponto em que h for
derivável.
Conclusão: Dada uma função h, qualquer outra função
f, cujo gráfico é obtido a partir do gráfico de h
através de uma translação
vertical, isto é, f(x)=h(x)+k,
onde k é uma constante, tem derivada em todos os pontos em que
h for derivável e, mais ainda,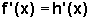 . Isso significa que em cada
. Isso significa que em cada 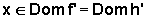 as retas tangentes aos gráficos de f e h têm o mesmo coeficiente
angular, isto é, são paralelas.
as retas tangentes aos gráficos de f e h têm o mesmo coeficiente
angular, isto é, são paralelas.
![]() Dada
f1(x)=(x+1)2, temos f'1=2.(x+1).
Dada
f1(x)=(x+1)2, temos f'1=2.(x+1).
![]() Se
Se 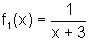 então
então
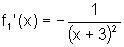 . É
possível generalizar esse fato, ou seja, se
. É
possível generalizar esse fato, ou seja, se 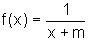 ,
onde m é uma constante, então
,
onde m é uma constante, então 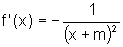 ?
?
![]() De modo geral, sendo h uma função derivável, se f(x)=h(x+m),
onde m é uma constante, então a derivada de f em cada x,
coincide com a derivada de h, calculada em x+m.
De modo geral, sendo h uma função derivável, se f(x)=h(x+m),
onde m é uma constante, então a derivada de f em cada x,
coincide com a derivada de h, calculada em x+m.
Conclusão: Dada uma função h, qualquer outra função
f, cujo gráfico é obtido a partir do gráfico de h
através de uma translação
horizontal, isto é, f(x)=h(x+m),
onde m é uma constante, tem derivada em todos os pontos em que
h for derivável e, mais ainda, 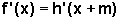 .
Isso significa que em cada
.
Isso significa que em cada 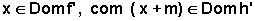 ,
as retas tangentes aos gráficos de f e h,
nos pontos de abscissa x e x+m, respectivamente, têm o mesmo coeficiente
angular, isto é, são paralelas.
,
as retas tangentes aos gráficos de f e h,
nos pontos de abscissa x e x+m, respectivamente, têm o mesmo coeficiente
angular, isto é, são paralelas.
![]() Se
Se 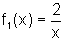 então
então
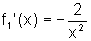 . É
possível generalizar esse fato, ou seja, se
. É
possível generalizar esse fato, ou seja, se 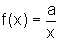 ,
onde a é uma constante, então
,
onde a é uma constante, então 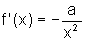 ?
?
![]() De modo geral, sendo h uma função derivável, se f(x)=a.h(x),
onde a é uma constante, então a derivada de f em cada x,
é igual à derivada de h, multiplicada pelo fator a.
De modo geral, sendo h uma função derivável, se f(x)=a.h(x),
onde a é uma constante, então a derivada de f em cada x,
é igual à derivada de h, multiplicada pelo fator a.
Conclusão: Dada uma função h, qualquer outra função
f, cujo gráfico é obtido a partir do gráfico de h
através de uma mudança
de inclinação, isto é, f(x)=a.h(x), onde a é
uma constante, tem derivada em todos os pontos em que h for derivável
e, mais ainda, 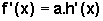 .
Isso significa que em cada
.
Isso significa que em cada 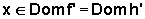 ,
as retas tangentes aos gráficos de f e h guardam entre si a seguinte
relação: o coeficiente angular da reta tangente ao gráfico
de f é igual ao coeficiente angular da reta tangente ao gráfico
de h multiplicado por a. Assim, quando a curva sofre
mudança de inclinação, a reta tangente também
sofre essa mudança, segundo o mesmo fator.
,
as retas tangentes aos gráficos de f e h guardam entre si a seguinte
relação: o coeficiente angular da reta tangente ao gráfico
de f é igual ao coeficiente angular da reta tangente ao gráfico
de h multiplicado por a. Assim, quando a curva sofre
mudança de inclinação, a reta tangente também
sofre essa mudança, segundo o mesmo fator.
![]() Sendo
Sendo 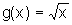 , a derivada
g' é dada por
, a derivada
g' é dada por 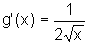 .
.
![]() Sendo h(x)=x2, definida para x não negativo, a
inversa da função g da Situação
10, é possível relacionar a derivada de h com
a derivada de g.
Sendo h(x)=x2, definida para x não negativo, a
inversa da função g da Situação
10, é possível relacionar a derivada de h com
a derivada de g.
![]() A Situação 11 pode ser generalizada para duas funções
que são uma a inversa da outra.
A Situação 11 pode ser generalizada para duas funções
que são uma a inversa da outra.
Conclusão: Dada uma função
f derivável, com derivada diferente de zero, sendo g sua inversa,
com 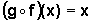 , temos
que os gráficos de f e g são simétricos em relação
à reta y=x. Então a derivada de g
em f(x) é igual ao inverso da derivada de f em x.
, temos
que os gráficos de f e g são simétricos em relação
à reta y=x. Então a derivada de g
em f(x) é igual ao inverso da derivada de f em x.
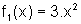 , então
, então
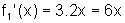 .
. 