Solução geométrica:

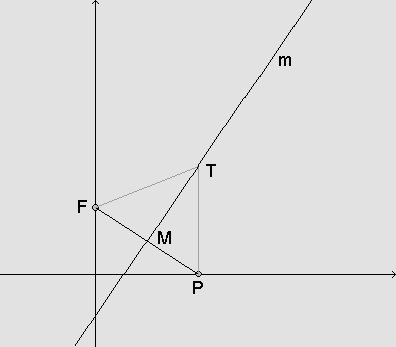
Sendo F=(0,2p) e P=(2a,0), consideremos a mediatriz m do segmento FP.

Precisamos mostrar que em m existe um único ponto que satisfaz à definição de parábola.

Vamos mostrar que esse ponto é exatamente aquele obtido ao levantar a perpendicular à diretriz e que passa pelo ponto P. Essa perpendicular encontra a mediatriz m num ponto T.

De fato, os triângulos TFM e TMP são congruentes, pois ambos têm um ângulo reto em M e FM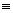MP, já que m é mediatriz. Além disso, o segmento MT é comum aos dois triângulos. Assim pelo caso LAL, os triângulos são congruentes.

Logo, os lados TF e TP são congruentes e, portanto, o ponto T está na parábola, pois satisfaz a definição dessa curva.

Qualquer outro ponto da reta m não pode estar na parábola, pois não satisfaz a condição de ser eqüidistante do foco e da diretriz. Verifique!

Portanto, T é ponto de tangência.

Para encontrar as coordenadas de T basta observar que sua abscissa é igual à de P, portanto, 2a. A ordenada de T pode ser obtida observando que T pertence à reta m.

Solução algébrica:

Sendo F=(0, 2p) e P=(2a, 0), temos:

·A equação da reta FP é: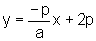
·A equação da mediatriz m de FP é: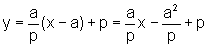
·A equação da parábola com diretriz o eixo x e foco (0, 2p) é:

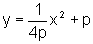
Devemos descobrir em que ponto a mediatriz intercepta a parábola:

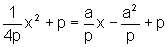
ou seja, resolvendo a equação do segundo grau, temos:

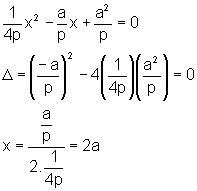
de onde concluímos que a reta m encontra a parábola em um único ponto:
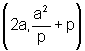, sendo portanto tangente à curva.