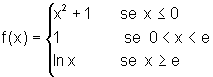Considere a função

Mostre que f é contínua em todo ponto de seu domínio. Decida em qual subconjunto de seu domínio, f é derivável. Dê a expressão e o gráfico de f'.

Invente uma função definida por partes - três ou quatro - como no Exercício 1, que seja contínua no domínio.

a) Construa seu gráfico.
b) Garanta a continuidade de sua função.
c) Decida em qual subconjunto do domínio, sua função é derivável.
d) Dê a expressão e o gráfico da derivada.

Invente uma outra função definida por partes - três ou quatro - como no Exercício 1, que seja derivável no domínio.

a) Construa seu gráfico.
b) Garanta a continuidade de sua função.
c) Garanta a derivabilidade de sua função.
d) Dê a expressão e o gráfico da derivada.

Descubra condições sobre os parâmetros a, b, c, m e n para que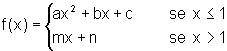

a) seja contínua em x=1;
b) seja derivável em x=1.
c) Dê um exemplo numérico de uma função derivável desse tipo.