Sendo 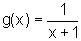, devemos encontrar o valor do limite que nos fornece o coeficiente angular da reta tangente ao gráfico de g em um ponto qualquer:

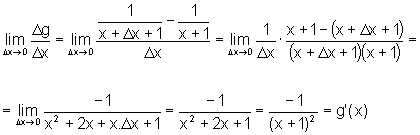
Assim, sendo 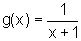, obtivemos .

Comparando com o Exercício 2, ond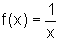e e 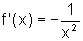, observamos que o resultado obtido para g' é natural se pensamos na translação horizontal sofrida pelo gráfico de g em comparação ao gráfico de f.

A fim de determinar a equação da reta tangente ao gráfico de g em (-7,4), observamos que a reta deve ser tangente à curva no ponto de tangência
(p, f(p)) e que deve passar pelo ponto (-7,4). De forma genérica, a equação da reta é a seguinte:

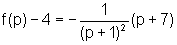
ou melhor,

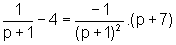
ou seja,

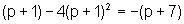
de onde,

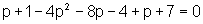
e, portanto,

.

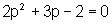Resolvendo a equação do segundo grau, temos:

,

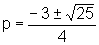de onde 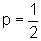ou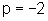

Encontramos assim, dois pontos de tangência: 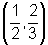e .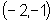

É interessante observar que cada um deles se encontra num dos ramos da hipérbole, uma vez qu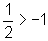e e .

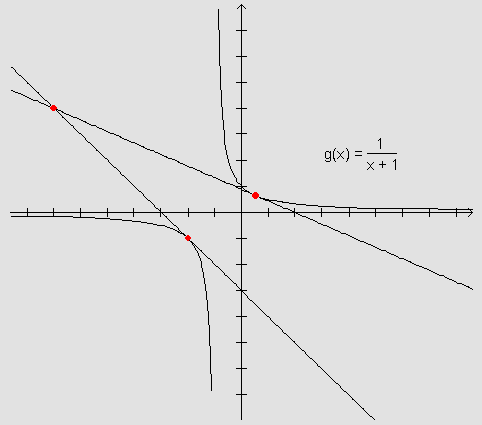
Podemos escrever as equações das retas tangentes ao gráfico de g e que passam pelo ponto (-7,4):

• No ponto de tangência 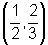, temos 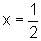, 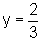e o coeficiente angular da reta é: .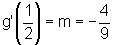

Logo, a equação da reta tangente é:

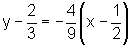ou

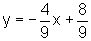
• No ponto de tangência (-2,-1), temos x=-2, y=-1 e o coeficiente angular da reta é: g'(-2)=m=-1.

Logo, a equação da reta tangente é:

y+1=-(x+2) ou y=-x-3